【Leetcode题解】Weekly Contest 339 周赛题目解析

Posted on Sun 02 April 2023 in Leetcode

这次周赛第四题难度陡增，但是前三题又较为手速。半个小时做完三题之后，盯着第四题想了一小时也还是毫无办法。最终第四题的AC率为100 / 5803 = 1.7%，真乃奇景……

题目列表

2609. Find the Longest Balanced Substring of a Binary String 最长平衡子字符串

给定二元字符串s，其中只有0和1，找到最长的字串符合特定条件： - 0和1的数量相等 - 0都在1的前面

考虑以下状态机

  • 记录0和1的个数。
  • 存在1的情况下，新的元素为0，记录最大的情况，并重设0和1的个数。
  • 最大的情况为0和1的个数其中较小的那个，长度为两倍。

代码

class Solution:
    def findTheLongestBalancedSubstring(self, s: str) -> int:
        result = 0
        zeros = 0
        ones = 0
        for c in s:
            if c == '0':
                # reset
                if ones > 0:
                    result = max(result, min(zeros, ones) * 2)
                    zeros = 0
                    ones = 0
                zeros += 1
            elif c == '1':
                ones += 1
        result = max(result, min(zeros, ones) * 2)

        return result

2610. Convert an Array Into a 2D Array With Conditions 转换二维数组

给定一个列表的数字nums，把他排列成一个二维数组，使得每一行都没有重复的元素。

标准的map题目。我们贪心的让前面的数组尽可能的排列更多的数字即可。

代码

from collections import Counter

class Solution:
    def findMatrix(self, nums: List[int]) -> List[List[int]]:
        result = [] # 2d array

        c = dict(Counter(nums))

        while c:
            sresult = []
            for k in c.keys():
                sresult.append(k)
                c[k] -= 1
            for k in sresult:
                if c[k] == 0:
                    del c[k]
            result.append(sresult)

        return result

2611. Mice and Cheese 老鼠和奶酪

给定两个数组reward1和reward2，和一个正整数k。reward1[i]和reward2[i]分别代表两只老鼠吃i种奶酪所得的分数。每种奶酪只能给一只老鼠吃并获得对应的分数。如果假设第一只老鼠只能吃k个奶酪的话，问最多可能得到的分数。注意这里没有限定第二只老鼠吃多少个，所以我们可以假设第二只老鼠把第一只老鼠吃剩的奶酪都吃了，也就是可以获得所有rewards2剩余的分数。这里有几位同僚可能看成两只老鼠都只能吃k个了，还是要注意审题啊。此外，rewards1和rewards2都是正整数。

这道题很明显是有某种最优子问题的解法，所以我们首先考虑dp。实际上这里可以对问题进行化简一下。假设我们让第二只老鼠吃掉所有的奶酪，那么我们可以获得reward2全部的分数。第一只老鼠每吃掉第i个奶酪，我们就要扣掉reward2[i]并加上reward1[i]。也就是说，实际上reward[2]可以看作是对于第一只老鼠的某个惩罚系数。我们期望吃到k个奶酪，使而惩罚系数尽可能小。这样的话，实际上就是某种线性系统的优化问题。因为只是线性的，局部最优可以是全局最优，因此我们考虑是否可以用贪心的方法来做。

实际上，如果我们定义吃第i个奶酪的效用为utility[i] = reward1[i] - reward2[i]的话，那么我们让第一只老鼠贪心地吃k个效用最大的，剩下的给第二个老鼠吃，这就是这道题的最优解。

代码

class Solution:
    def miceAndCheese(self, reward1: List[int], reward2: List[int], k: int) -> int:
        total_r2 = sum(reward2)
        diff = [(i, reward1[i] - reward2[i]) for i in range(len(reward1))]

        diff.sort(key=lambda x: -x[1])

        # print(diff)

        result = total_r2
        for i in range(k):
            idx, _ = diff[i]
            result += reward1[idx] - reward2[idx]

        return result

2612. Minimum Reverse Operations 最少翻转操作数

给定一个整数n为一个数组的长度，这个数组arr是一个只有-1, 0, 1的数组。整数p为一个索引，表示arr[p] = 1。banned为一个索引列表，表示arr[banned[i]]不可变化，永远为0。给定一个数字k，现在你可以对arr做任意次数的翻转操作，如arr = [1,0,1,0,1], k = 2，可以反转arr[1:3]使得新数组为[1,1,0,0,1]。除此之外，如果arr某一个数字是banned的话，翻转操作无效。如arr = [1,0,1,0,1], k = 4, banned = [3]，翻转arr[1:5]使得新数组为[1,1,0,0,0]。即banned里面的数组索引所在的数字永远为0不可改变，但是可以翻转到别的位置上去。最后要求你返回一个数组ans使得ans[i]为arr[i]变为0最少需要翻转多少次；若i为banned或者永远无法到达的话，则ans[i] = -1。

这道题还是有点难度的，读题理解题目就花费了我不少时间。在限定时间内写出正确答案的话对于正常人来说还是比较难的。首先，我们可以很快发现，对于这道题来说，他其实像一个图的题目。仔细思考一下，通过对于某个子数组进行翻转，我们可以把1移动到另一个位置上，因此这就是图一条边。但是，如果要构造对应的图来说，比较难一点。我们先来看几个例子，例子里面我们通过翻转操作，找一次翻转可以到的位置。此外，我们先不管banned这个条件，因为他就是要用这个条件来迷惑你的。

Example 1
Input: p = 4, arr = [0,0,0,0,1,0,0,0], k = 5
Output: [0, 2, 4, 6]
Explanation:
- flip [0:5], arr = [1,0,0,0,0,0,0,0] => 0
- flip [1:6], arr = [0,0,1,0,0,0,0,0] => 2
- flip [2:7], arr = [0,0,0,0,1,0,0,0] => 4
- flip [3:8], arr = [0,0,0,0,0,0,1,0] => 6

这里我们看到，当p = 4，k = 5的时候，我们的索引应该是[0, 2, 4, 6(, 8)]（如果arr再长一点的话）。再看一个偶数的例子吧。

Example 2
Input: p = 4, arr = [0,0,0,0,1,0,0,0], k = 4
Output: [1,3,5,7]
Explanation: 
- flip [1:5], arr = [0,1,0,0,0,0,0,0] => 1
- flip [2:6], arr = [0,0,0,1,0,0,0,0] => 3
- flip [3:7], arr = [0,0,0,0,0,1,0,0] => 5
- flip [4:8], arr = [0,0,0,0,0,0,0,1] => 7

那么在边界的时候，我们怎么处理呢？

Example 3
Input: p = 1, arr = [0,1,0,0,0,0,0,0], k = 5
Output: [3, 5]
Explanation:
- flip [0:5], arr = [0,0,0,1,0,0,0,0] => 3
- flip [1:6], arr = [0,0,0,0,0,1,0,0] => 5

Example 4
Input: p = 6, arr = [0,0,0,0,0,0,1,0], k = 5
Output: [3, 5]
Explanation:
- flip [2:7], arr = [0,0,1,0,0,0,0,0] => 2
- flip [3:8], arr = [0,0,0,0,1,0,0,0] => 4

这里直接给公式吧。

$$ lo=\begin{cases} i - (k - 1) & i > (k - 1) \\ (k - 1) - i & \text{otherwise} \end{cases} $$

对于我们的左边界来说比较好理解，就是abs(i - (k - 1))。

$$ hi=\begin{cases} i + (k - 1) & i + (k - 1) < n \\ i + 2*(n - i - 1) - (k - 1) & \text{otherwise} \end{cases} $$

对于我们的右边界来说，如果 i + (k - 1)越界了的话，需要一点点特殊处理。这里可以看下面的草图，我们算出i + (k - 1)在越界之后的映射（下面的小红点的位置），可以做一个延长线。当然，这个技巧有点超纲了……

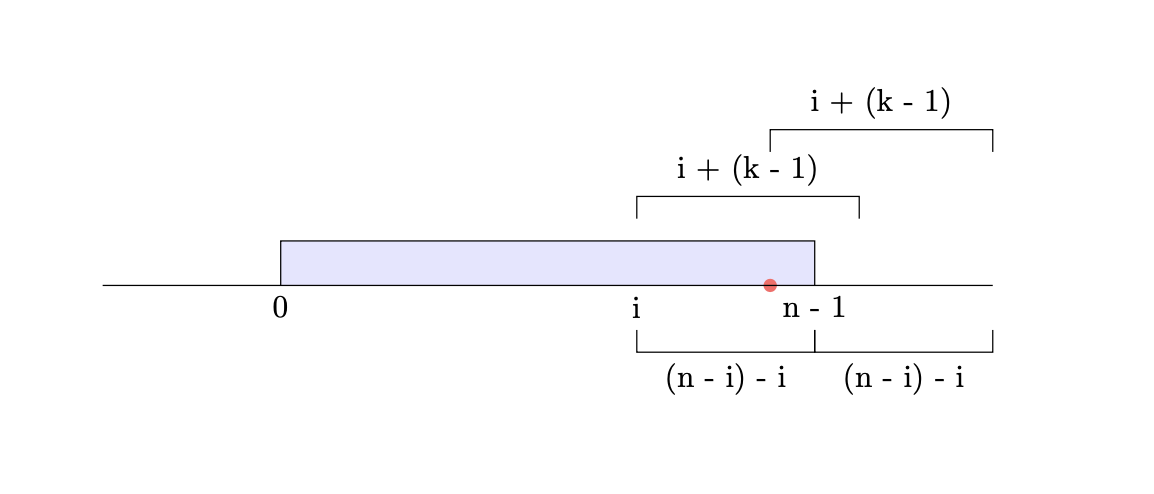
总之，回到我们的topic。既然我们有了lo和hi上下界，我们是不是直接遍历里面间隔一个数的点就好了呢？我们算出来的[lo, hi]的界限可能会非常大，因此遍历是行不通的。我们这里考虑一个sortedset能够直接通过上下界查询并遍历里面的元素。此外，lo的奇偶性决定了我们是选择奇数的点还是偶数的点，所以我们可以用两个set来分别维护，根据lo的奇偶性来解决。不要忘记了，我们还有一个被遗忘的banned列表，在我们构建set的时候要把他们排除掉。

代码

from sortedcontainers import SortedList

class Solution:
    def minReverseOperations(self, n: int, p: int, banned: List[int], k: int) -> List[int]:
        result = [-1] * n
        result[p] = 0

        remaining = [SortedList(), SortedList()]

        banned = set(banned)

        for i in range(n):
            if i in banned:
                continue
            if i == p:
                continue
            remaining[i & 1].add(i)

        queue = deque()

        queue.append(p)

        while queue:
            i = queue.popleft()

            lo = max(i - (k - 1), (k - 1) - i)

            hi = min(i + (k - 1), i + 2*(n - i - 1) - (k - 1))

            # print(remaining[lo & 1], i, lo, hi, list(remaining[lo & 1].irange(lo, hi)))

            for nei in list(remaining[lo & 1].irange(lo, hi)):
                queue.append(nei)
                result[nei] = result[i] + 1
                remaining[lo & 1].remove(nei)


        return result

小结

这次周赛第四题难度陡增。看别人分析，基本达到了codeforces div2的D题程度1，AC的大佬的LC Rating都在2600左右。所以，对于咱们普通人来说，三题AC就已经很好了！面试应该不会出这种题吧（笑）。

如果你想变得更强的话，可以做做

附录

上面图片的LaTeX icon代码 
\documentclass{article}
\usepackage{graphicx} % Required for inserting images
\usepackage{tikz}
\usepackage{xcolor}

\begin{document}

\begin{tikzpicture}
% the array length
\draw[fill=blue!10](-3,0) node[below] {0} -- (-3,0.5) -- (3, 0.5) -- (3, 0) node[below]{n - 1};

% vertical line at i
\draw (1, 0) node[below]{i} ;

% original i + (k - 1)
\draw (1, 0.75) -- (1, 1) -- (3.5, 1) -- (3.5, 0.75);
\draw (2.25, 1) node[above]{(k - 1)};
% offseted i + (k - 1) 
\draw (2.5, 1.5) -- (2.5, 1.75) -- (5, 1.75) -- (5, 1.5);
\draw (3.75, 1.75) node[above]{(k - 1)};

% the point we look for
\node at (2.5, 0) [circle, fill=red!60, inner sep=1.5]{};

% n - 1 - i
\draw (1, -0.5) -- (1, -0.75) -- (3, -0.75) -- (3, -0.5);
\draw (2, -0.75) node[below]{(n - 1) - i};
\draw (3, -0.5) -- (3, -0.75) -- (5, -0.75) -- (5, -0.5);
\draw (4, -0.75) node[below]{(n - 1) - i};

% the axis
\draw[-] (-5,0)--(5,0);
\end{tikzpicture}

\end{document}
  1. CF的难易度分析见这篇文章 ↩

Contest