【Leetcode题解】2604. Minimum Time to Eat All Grains

Posted on Fri 07 April 2023 in Leetcode

今日闲来无事，简单做一下2604. Minimum Time to Eat All Grains

题目首先给定两个数字列表hens和grains。hens代表鸡的位置，grains代表饲料的位置。每只鸡可以吃掉无限的饲料；在位置i的鸡可以立即吃掉当前位置的饲料。但如果鸡的位置不等于饲料的位置的话，鸡可以移动过去吃饲料，且每秒移动速度是1。所有的鸡可以同时移动且互相独立。假定所有鸡都按照最优方法移动的话，我们需要找到最短时间使得所有饲料都可以被吃掉。

这道题我第一个思路是先找到一些比较小的子问题，来进行求解。显然，这道题有两个最小的子问题，即有1只鸡和多个饲料，或者多只鸡和1个饲料的例子。

Example 1
Input: hens = [6], grains = [2, 8]
Output: 8
Explanation:
One way to move
hens 0 move 6 -> 8 => 2s
hens 0 move 8 -> 2 => 6s
Another way to move
hens 0 move 6 -> 2 => 4s
hens 0 move 2 -> 8 => 6s

上面我们可以看到，如果一只鸡旁边有两个饲料的话，需要优先吃距离最短的，这样才能使得整体距离最小。

Example 2
Input: hens = [1, 10], grains = [7]
Output: 3
Explanation:
One way to move
hens 0 move 1 -> 7 => 6s
Another way to move
hens 1 move 10 -> 7 => 3s

第二个例子也是要用相同的方法，即我们试着让离饲料最近的鸡去吃就能拿到最优解。

这里我们只讨论了限制最大的两种情况。当我们有多只鸡和多个grain的情况的时候就不太好办了。思路到这里就断了。那么，我们能不能把时间这个变量固定住，再检查是否能在固定时间内完成我们的条件呢？我们要求的是最短的时间T = t。简单推理下可知，且当T < t的时候都无法完成，T > t的时候都可以完成。当然一个一个时间点查看肯定会超时，这里我们采用二分来找。

那么剩下的问题就是怎么判断在给定时间T里面判断是否可以吃到全部的饲料了。这里优先考虑对hens和grains进行排序，我们再一个个进行匹配。给定一只鸡的位置h和时间t，我们想要找到离他最近的饲料并标记这些饲料被他吃掉了。我们从小到大开始循环，我们有这么两条条规则

如果有饲料g在h左边的话，必须要吃掉。
剩余时间需要尽量向右移动吃右边的饲料。

但是我们发现，在规则1中，如果右边的饲料比左边更近的话，先移动到左边不一定最优，就如同上面的例子1中，我们先吃左边的比先吃右边的耗时更久。因此，我们进一步展开规则为

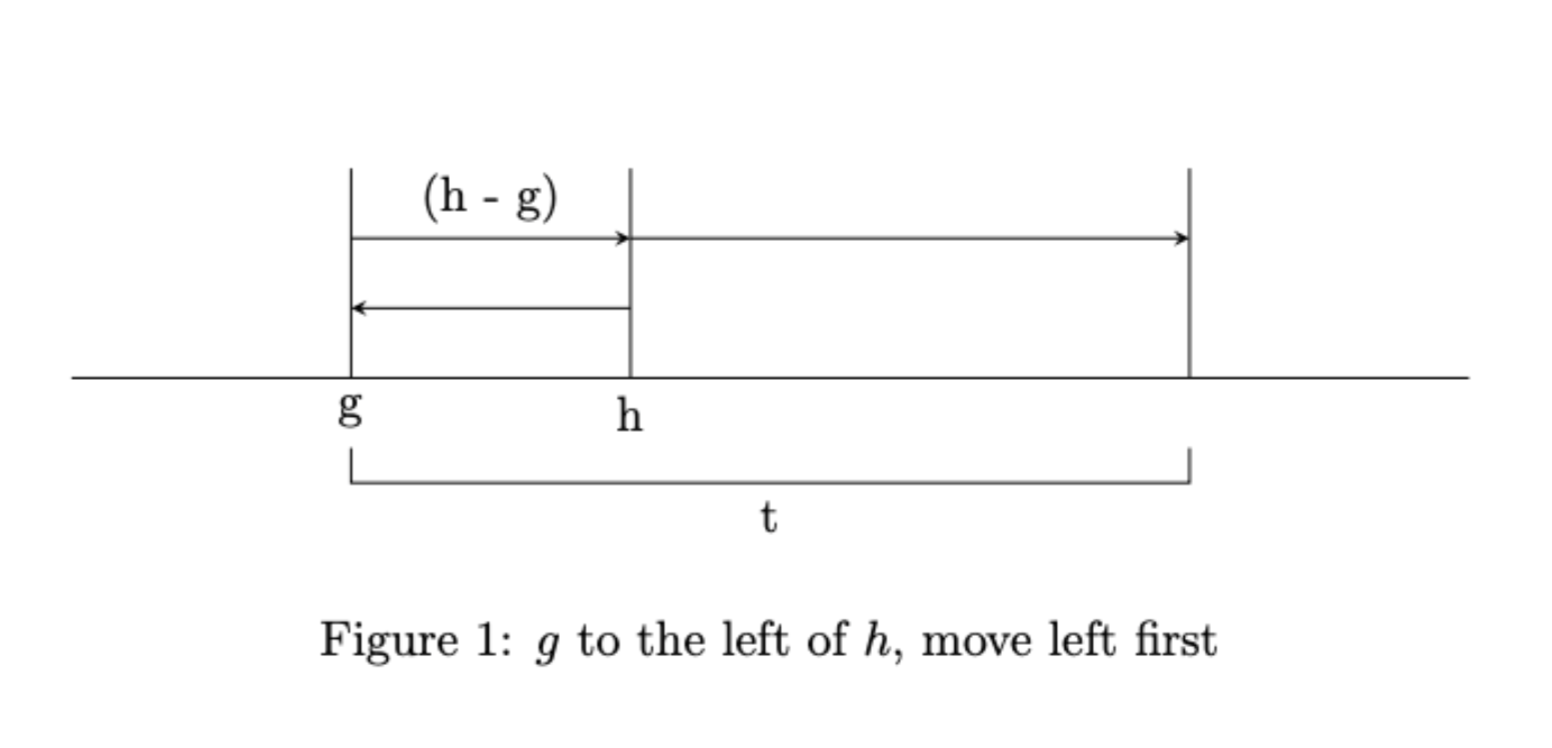
左边有饲料g的情况下，我们先移动h到左边，然后回到g，可以移动到最右边的距离为t - 2 * (h - g)
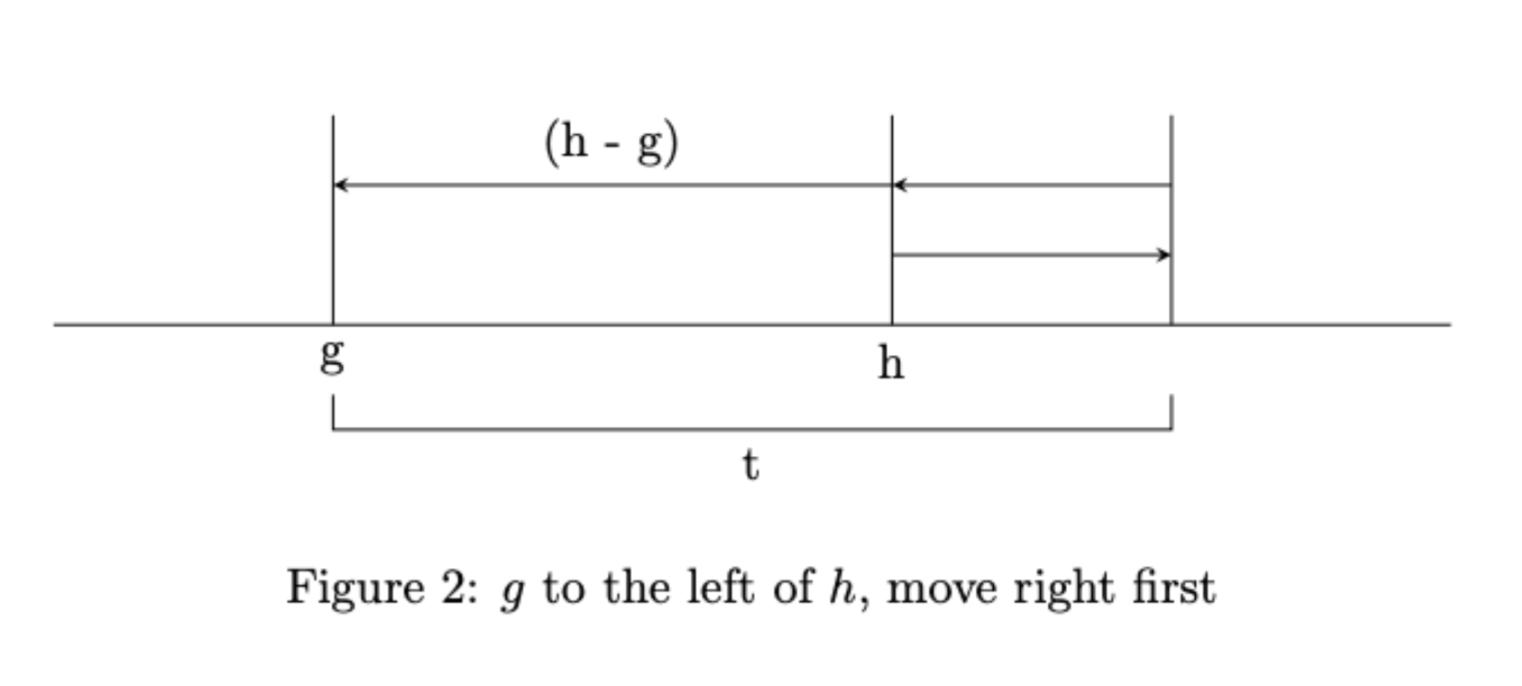
左边有饲料g的情况下，我们先移动h到右边，最后回到g，可以移动到最右边的距离为(t - (h - g)) / 2。
左边没有饲料的情况下，可以移动到最右边的距离为t。

代码

class Solution:
    def minimumTime(self, hens: List[int], grains: List[int]) -> int:
        def check(t):
            idx = 0
            for h in hens:
                move = t
                # if there are grains left of h
                # need to eat left
                if grains[idx] < h:
                    left_cost = h - grains[idx]
                    if left_cost > t:
                        return False
                    # move left and back to original position
                    # move right then move back to left
                    # whichever way is further
                    move = max(0, t - 2 * left_cost, (t - left_cost) // 2)

                if h + move >= grains[idx]:
                    idx = bisect_right(grains, h + move, lo = idx)
                    if idx == len(grains):
                        return True
            return False

        hens.sort()
        grains.sort()
        l = 0
        r = 2 * (max(grains[-1], hens[-1]) - min(grains[0], hens[0]))
        while l < r:
            mid = (l + r) // 2
            if check(mid):
                r = mid
            else:
                l = mid + 1
        return l

附录

上面图片的

代码

\documentclass{article}
\usepackage{graphicx} % Required for inserting images
\usepackage{tikz}
\usepackage{xcolor}
\pagenumbering{gobble}

\begin{document}


\begin{figure}
\centering
\begin{tikzpicture}
% 2 * (h - g)
\draw (-2, 1) node[above]{(h - g)};
\draw [stealth-](-1,1) -- (-3,1);
\draw [-stealth](-1,0.5) -- (-3,0.5);
% t - 2 * (h - g)
\draw [-stealth](-1, 1) -- (3, 1);
\draw (3, 1.5) -- (3, 0);
% t
\draw (-3, -0.5) -- (-3, -0.75) -- (3, -0.75) -- (3, -0.5);
\draw (0, -0.75) node[below]{t};
% g
\draw (-3, 1.5) -- (-3, 0) node[below]{g};
% h
\draw (-1, 1.5) -- (-1, 0) node[below]{h};
% the axis
\draw[-] (-5,0)--(5,0);
\end{tikzpicture}
\caption{$g$ to the left of $h$, move left first}
\end{figure}

\begin{figure}
\centering
\begin{tikzpicture}
% (h - g) 
\draw (-1, 1) node[above]{(h - g)};
\draw [stealth-](-3,1) -- (1,1);
% (t - (h - g)) // 2
\draw [-stealth](1, 0.5) -- (3, 0.5);
\draw [stealth-](1, 1) -- (3, 1);
\draw (3, 1.5) -- (3, 0);
% g
\draw (-3, 1.5) -- (-3, 0) node[below]{g};
% h
\draw (1, 1.5) -- (1, 0) node[below]{h};
% t
\draw (-3, -0.5) -- (-3, -0.75) -- (3, -0.75) -- (3, -0.5);
\draw (0, -0.75) node[below]{t};

% the axis
\draw[-] (-5,0)--(5,0);
\end{tikzpicture}
\caption{$g$ to the left of $h$, move right first}
\end{figure}

\begin{figure}
\centering
\begin{tikzpicture}
\draw [-stealth](-3, 0.5) -- (3, 0.5);
% g
\draw (3, 1.5) -- (3, 0) node[below]{g};
% h
\draw (-3, 1.5) -- (-3, 0) node[below]{h};
% t
\draw (-3, -0.5) -- (-3, -0.75) -- (3, -0.75) -- (3, -0.5);
\draw (0, -0.75) node[below]{t};
% the axis
\draw[-] (-5,0)--(5,0);
\end{tikzpicture}
\caption{$g$ to the right of $h$, move right}
\end{figure}

\end{document}