解决Foobar挑战（一）

Foobar系列已经全部完成了，你可以通过以下目录访问！

• 解决Foobar挑战（一）
• 解决Foobar挑战（二）
• 解决Foobar挑战（三）
• 解决Foobar挑战（四）- 终篇

Google用Foobar挑战来甄选人才已经是一个半公开的秘密了。在搜索框里输入一些特定的程序语言关键词，或者是查看Google产品的开发者文档的时候，你有几率在某个角落里找到一个奇怪的图标。点击这个图标，就进入了Foobar挑战的流程。在这个过程中，你需要在限时内完成一定数量的代码题目，然后Google会视完成情况向你发出面试邀请。不得不说这个行为非常的Geek。数年前，笔者有幸触发了一次Foobar挑战，但是并没有完成。今天在浏览互联网上的信息的时候，突然发现自己还是可以登入Foobar挑战的页面，并且接着上次的进度继续完成挑战，于是便有了这篇博文。

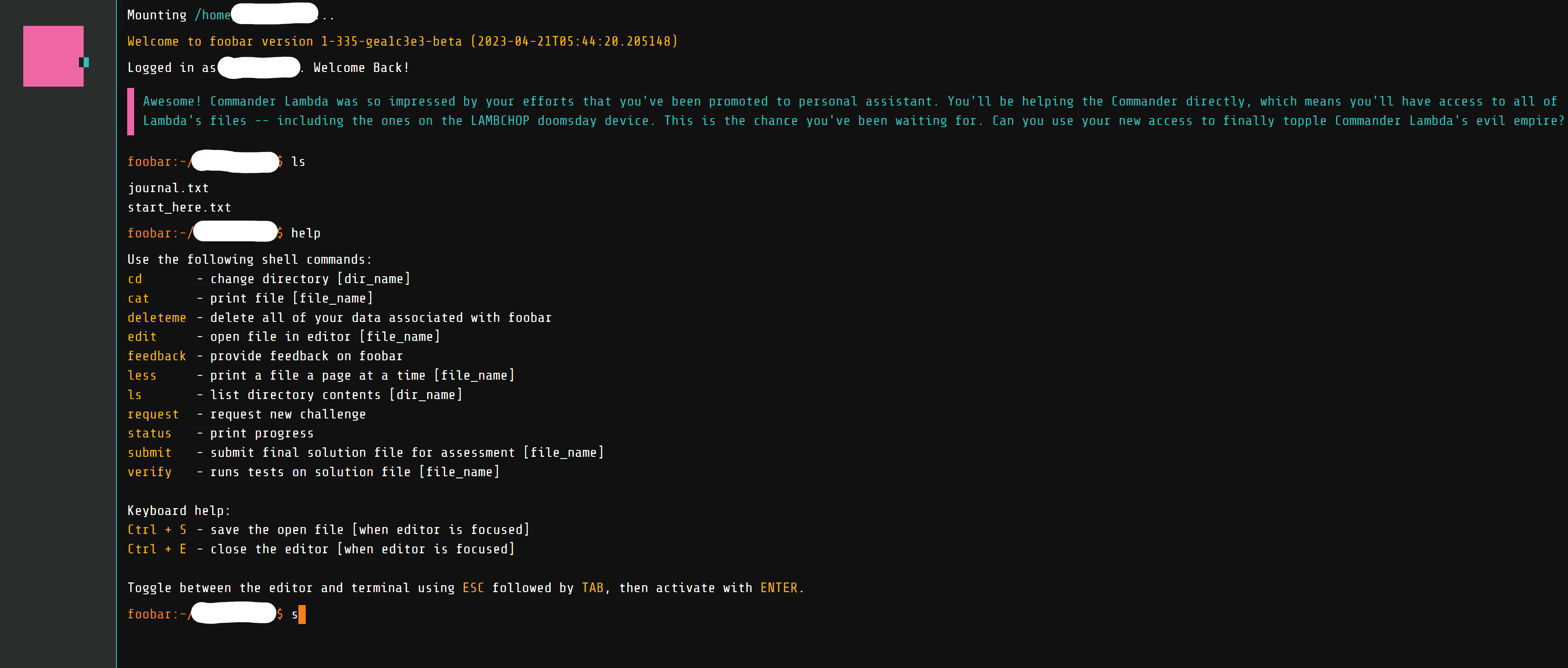
Foobar的页面一进去就是一个炫酷的命令行界面。在这里你可以输入一些命令去查看当前挑战进度，请求新的挑战题目，提交答案等等。总共有五层挑战，而且众所周知的，每一层挑战都比上一层难度会提升。每道题的时间都给的非常充裕，你会有7天左右的时间去完成每一道题目。接着上次的进度，我进入了第二题的流程。输入request便收集到了第二题的题目。让我们一起看看吧。

Gearing Up for Destruction

As Commander Lambda's personal assistant, you've been assigned the task of configuring the LAMBCHOP doomsday device's axial orientation gears. It should be pretty simple -- just add gears to create the appropriate rotation ratio. But the problem is, due to the layout of the LAMBCHOP and the complicated system of beams and pipes supporting it, the pegs that will support the gears are fixed in place.

The LAMBCHOP's engineers have given you lists identifying the placement of groups of pegs along various support beams. You need to place a gear on each peg (otherwise the gears will collide with unoccupied pegs). The engineers have plenty of gears in all different sizes stocked up, so you can choose gears of any size, from a radius of 1 on up. Your goal is to build a system where the last gear rotates at twice the rate (in revolutions per minute, or rpm) of the first gear, no matter the direction. Each gear (except the last) touches and turns the gear on the next peg to the right.

Given a list of distinct positive integers named pegs representing the location of each peg along the support beam, write a function solution(pegs) which, if there is a solution, returns a list of two positive integers a and b representing the numerator and denominator of the first gear's radius in its simplest form in order to achieve the goal above, such that radius = a/b. The ratio a/b should be greater than or equal to 1. Not all support configurations will necessarily be capable of creating the proper rotation ratio, so if the task is impossible, the function solution(pegs) should return the list [-1, -1].

For example, if the pegs are placed at [4, 30, 50], then the first gear could have a radius of 12, the second gear could have a radius of 14, and the last one a radius of 6. Thus, the last gear would rotate twice as fast as the first one. In this case, pegs would be [4, 30, 50] and solution(pegs) should return [12, 1].

The list pegs will be given sorted in ascending order and will contain at least 2 and no more than 20 distinct positive integers, all between 1 and 10000 inclusive.

给定一个整数列表pegs，代表在墙上的销子的位置。你需要在每一个销子上都放置一个齿轮且这些齿轮都互相咬合。每个齿轮的大小可以为任意数字，但是至少要为1。找到一种排列方式，使得最后一个齿轮的旋转速度是第一个齿轮的两倍，并返回第一个齿轮的大小。由于返回值可能不是一个正整数，你需要返回一个数组列表[m,n]代表m/n。如果给定的pegs无法找到一个符合条件的组合，则应该返回[-1, -1]。

题目看上去挺唬人的。先是一下子给了两百字的故事类的文字描述，接着引入了齿轮咬合这个大多数人看起来生疏的概念。我们简单进行建模一下。在这里我们暂时不需要考虑一些特别的参数，如齿轮的齿数如何影响咬合。就考虑一个真空中的球形鸡的模型：给定两个齿轮a和b，可知两个齿轮的半径和等于这两个齿轮之间的销子长度；若需要齿轮b的角速度是齿轮a的两倍，那么齿轮a的半径应该是齿轮b的两倍。我们可以拓展我们的模型到三个齿轮。给定三个齿轮a，b和c，他们的位置分别在销子\(p_a\), \(p_b\)和\(p_c\)上，此外我们还知道销子之间的距离\(D_x\)可以表示为

则可得

化简可得

又因\(r_a = 2 r_c\)，因此我们可以把\(r_a\)表示为

倘若我们有四个齿轮，我们也可以用同样的方式进行化简

化简可得

同样可知\(r_a = 2 r_d\)，因此

到这里我们就找出了这道题的规律。接下来就该设计算法了。我们简单分为三步：

1. 首先算出distance，即pegs之间的差值
2. 对于算出distance偶数索引的和和奇数索引和之间的差值，并根据distance的奇偶性求得前面的乘数。
3. 最后校验所有齿轮是否符合齿轮大小的要求。

且慢，这题还有个要求是要输出一个分数而不是浮点数。若存在2/3的乘数的话，我们应该把他进行化简。这里使用Python的同学有福了，可以直接用fractions.Fraction进行计算，f.numerator可得出分母，f.denominator为分子。对于其他语言的同学来说呢，既可以使用最大公约数gcd来化简分子和分母，也可以用浮点数近似到精度来处理。这里就不展开了。

代码

from fractions import Fraction

def solution(pegs):
    # Calculate the distances between pegs
    distances = [pegs[i+1] - pegs[i] for i in range(len(pegs) - 1)]

    # print(distances)

    radius = sum(distances[::2]) - sum(distances[1::2])

    if len(distances) % 2 == 0:
        radius *= Fraction(2, 1)
    else:
        radius *= Fraction(2, 3)

    if radius < 1:
        # print("less", radius)
        return [-1, -1]

    cradius = radius
    for d in distances:
        cradius = d - cradius
        if cradius < 1:
            # print("less intermediate", cradius, radius)
            return [-1, -1]

    return [radius.numerator, radius.denominator]

Hey, I Already Did That!

Commander Lambda uses an automated algorithm to assign minions randomly to tasks, in order to keep minions on their toes. But you've noticed a flaw in the algorithm -- it eventually loops back on itself, so that instead of assigning new minions as it iterates, it gets stuck in a cycle of values so that the same minions end up doing the same tasks over and over again. You think proving this to Commander Lambda will help you make a case for your next promotion.

You have worked out that the algorithm has the following process:

1. Start with a random minion ID n, which is a nonnegative integer of length k in base b
2. Define x and y as integers of length k. x has the digits of n in descending order, and y has the digits of n in ascending order
3. Define z = x - y. Add leading zeros to z to maintain length k if necessary
4. Assign n = z to get the next minion ID, and go back to step 2

For example, given minion ID n = 1211, k = 4, b = 10, then x = 2111, y = 1112 and z = 2111 - 1112 = 0999. Then the next minion ID will be n = 0999 and the algorithm iterates again: x = 9990, y = 0999 and z = 9990 - 0999 = 8991, and so on.

Depending on the values of n, k (derived from n), and b, at some point the algorithm reaches a cycle, such as by reaching a constant value. For example, starting with n = 210022, k = 6, b = 3, the algorithm will reach the cycle of values [210111, 122221, 102212] and it will stay in this cycle no matter how many times it continues iterating. Starting with n = 1211, the routine will reach the integer 6174, and since 7641 - 1467 is 6174, it will stay as that value no matter how many times it iterates.

Given a minion ID as a string n representing a nonnegative integer of length k in base b, where 2 <= k <= 9 and 2 <= b <= 10, write a function solution(n, b) which returns the length of the ending cycle of the algorithm above starting with n. For instance, in the example above, solution(210022, 3) would return 3, since iterating on 102212 would return to 210111 when done in base 3. If the algorithm reaches a constant, such as 0, then the length is 1.

Your code should pass the following test cases. Note that it may also be run against hidden test cases not shown here.

Input: solution.solution('1211', 10) Output: 1

Input: solution.solution('210022', 3) Output: 3

给定一个b进制，长度为k的数字z，我们需要对其应用一个算法

1. 定义x为这个数字z所有的位数降序排列。
2. 定义y为这个数字z的所有位数升序排列。
3. 计算z = x - y。
4. 重复这个过程直到我们遇到所有数字的循环。

最终我们应该返回这个环的长度。

这里我们直接进行模拟去找他的环。首先我们需要转换进制的工具。python并没有提供任意底数的转换，所以我们自己简单写一下字符串转base的工具，之后就按照题意进行模拟。而对于环的检测，我们直接用一个map记录每一个数字出现的索引。若我们重复遇到之前遇到的z的话，我们就遇到了一个环，而环的长度为当前索引减去之前遇到的索引。

实际上，数学家D. R. Kaprekar在1955年对这个性质进行研究，发现对于任意十进制四位数，通过上述变换，最多进行7次就会得到6174，因此这个数字也被称为Karprekar常数。有兴趣的朋友可以看一下这篇文章，讨论了对于三位数字进行上述变换会收敛到495的性质。

代码

def to_base_10(n, b):
    """Converts a string `n` in base `b` to an integer in base 10."""
    result = 0
    for digit in n:
        result = result * b + int(digit)
    return result


def from_base_10(n, b):
    """Converts an integer `n` in base 10 to a string in base `b`."""
    if n == 0:
        return '0'
    result = ''
    while n > 0:
        digit = n % b
        result = str(digit) + result
        n //= b
    return result


def solution(n, b):
    k = len(n)
    seen = {}
    i = 0
    while n not in seen:
        seen[n] = i
        x = ''.join(sorted(n, reverse=True)).rjust(k, '0')
        y = ''.join(sorted(n)).rjust(k, '0')
        z = from_base_10(to_base_10(x, b) - to_base_10(y, b), b).rjust(k, '0')
        # print(n, "->", x, "-", y, "=", z)
        n = z
        i += 1
    return i - seen[n]

小结

第二层的题目难度不高，但是总体来讲比较考验出题者对于题目的理解，并将题目进行拆解。两题都是比较偏向模拟的题目。此外，给的时间都很充裕，能让参赛者有充足的时间去学习和研究这道题目，并给出正确的解法，而不单单像是一个限时的OJ。

这里是一些参考文献：

• Wikipedia - 6174 (number)
• Everything You Need to Know About Google Foobar Challenge