Airline Empire之使用二次规划解决航线的最佳座位排布
Posted on Mon 21 August 2023 in Computer Science
Airline Empires(下称AE)是一款在线的航空公司经营类游戏。在游戏中,玩家将以上帝视角运营航线,覆盖各个地区,并与其他玩家展开竞争。游戏的节奏设计较为缓慢,每个游戏内的一天相当于现实时间的5至20分钟,使其成为一款休闲的模拟经营游戏。尽管游戏以纯文字形式呈现,没有任何视觉效果,但AE提供了丰富多样的飞机选择。运营航线需要考虑诸多因素,包括机场距离、飞机航程、跑道长度、座位布局以及不同舱位的定价策略。通过丰富的经营元素和策略考量,AE成功地为玩家提供了一个新奇的航空公司体验。无论是追求利润最大化还是航线网络的扩张,玩家都能在AE中找到乐趣与挑战。
游戏由一些爱好者团队进行维护,游玩是免费的,仅通过少量的贴片广告进行变现以支持游戏的运营。然而这也意味着玩家必须忍受小霸王服务器的卡顿。但是话又说回来了,免费又制作精良的游戏,还有专人进行维护,社区氛围也不错的游戏,要什么自行车呢?
笔者早在2018年就玩了这款游戏,期间也偶尔会回去重温一下。买上几架笔者最喜欢的麦道MD-80 (道格拉斯 DC-9)和道格拉斯DC-10,运营几条长航线,感觉非常满足。但今天这篇文章的目的不是介绍这款游戏本身,而是以AE的参数配置为起点来探索如何通过最佳的座位安排以获取收益。首先我会介绍这个游戏中如何配置航线和盈利,接着我会介绍我是如何通过建模来确定特定航线的最佳座位配置,并提供相应的代码供大家参考。
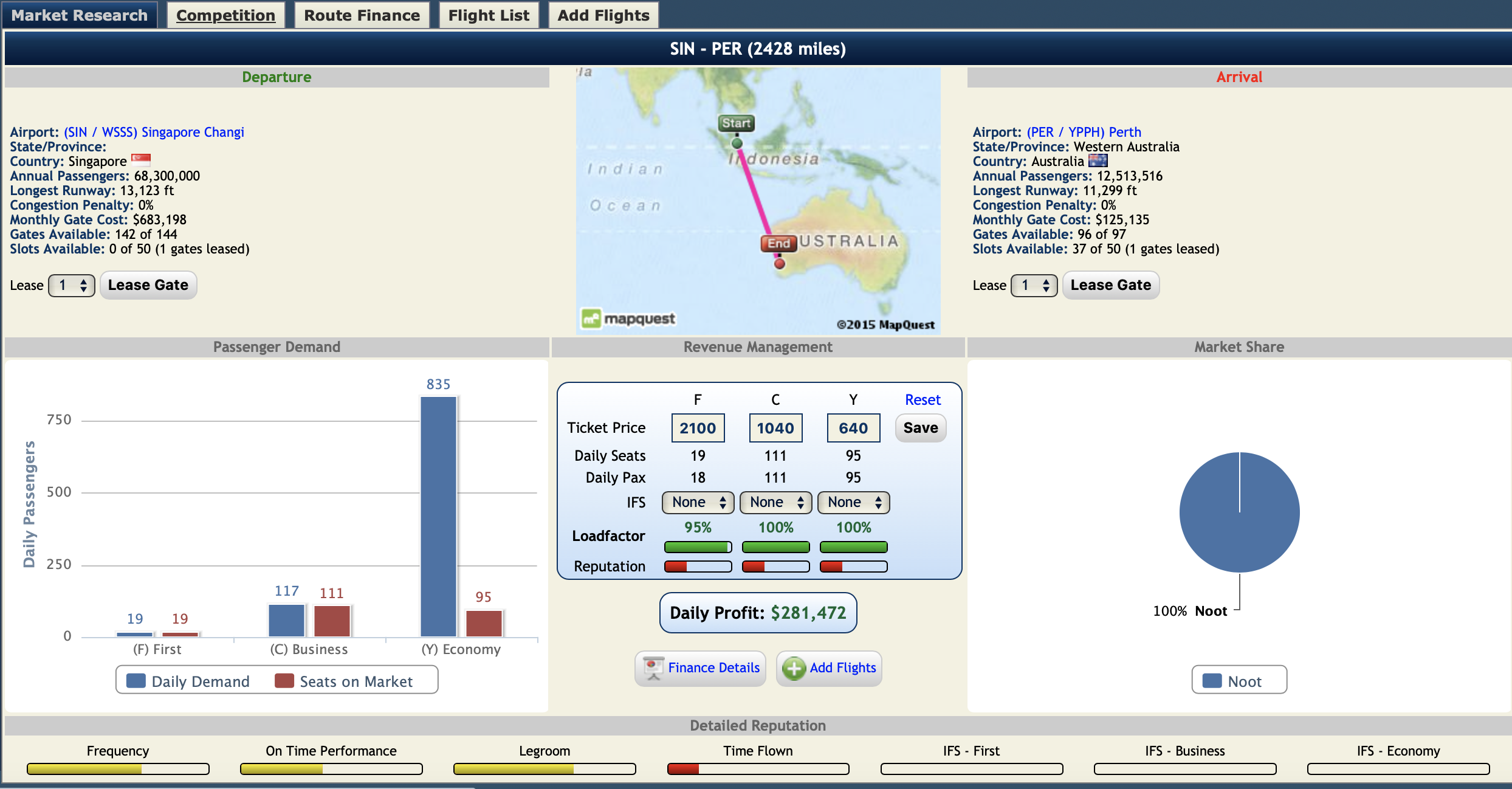
以从新加坡飞往珀斯的航线为例,航程全长2428英里(3907公里)。当前我们使用编号为58的麦道MD-83客机执飞,每周执飞26班。MD-83最多可容纳172名乘客,在4F10C146Y共160名乘客的座舱配置下,每周的盈利约为$246,014。但是这个仓位数量是我随手拍的一个值,并没有任何的依据。
如果我们能够根据航线的情况来定制各个仓位的座位数量,那么我们就能大幅度提高我们的盈利能力了。早在 2018 年,当我第一次玩这个游戏时,我就设想过这种优化,但缺乏相关的知识去真正把这个模型实现出来。但是到了2023年的今天,我已经掌握了足够的知识去实现程式化地计算了,让我们来一起看看我们到底如何建模吧。
首先我们要明确,我们的目标是预测某条特定航线上使用特定机型执飞的座位数量。此外,我们还要做一些假设
- 客流:因为游戏中上帝视角的存在,我们知道每条线路上各个仓位的每周客流数量。
- 机型:一架飞机每周的飞行时间是固定的,航线耗时和飞机转场时间决定了一条航线上每周最多只能飞多少次。
- 价格:在虽然游戏允许我们自由设定机票价格,但在我们的预测模型中,我们暂时将价格视为已知变量。
接着我们要明确我们的优化目标。我们有四个优化变量:头等舱、商务舱和经济舱的座位数X = (x, y, z),以及每周执飞航班数量n。我们的优化目标为各个仓位的收入的总和。此外,我们还会需要有一些额外的条件,这些条件包括
- 飞机载荷利用率:我们至少应当用到
90%以上的飞机载荷。 - 每周飞行航班量:我们的每周执飞航班数量不能超过最大执飞航班数量。此外,我们还可以藉由此变量控制多少架飞机飞这条航线 -- 只需将每架飞机的最大飞行次数乘以飞机总数即可。
- 仓位客流数量:每班飞机每周提供的座位数不应超过每周乘客人数,因为超过这一限制将不会产生额外收入。
有了这些之后,我们就可以开始实现我们的优化模型了。我们采用Gurobi来实现我们的方法。首先我们定义一个模型,按照我们上面描述的目标定义描述四个整数变量。
# Create a Gurobi model
model = gp.Model("SeatOptimization")
# Decision variables
x = model.addVar(vtype=gp.GRB.INTEGER, name="x")
y = model.addVar(vtype=gp.GRB.INTEGER, name="y")
z = model.addVar(vtype=gp.GRB.INTEGER, name="z")
n = model.addVar(vtype=gp.GRB.INTEGER, name="n")
接着我们加入刚刚所说的飞机空间利用率的限制。在游戏中,每个飞机有一个最大旅客载荷,且各个仓位与占载荷比例分别为(2.5, 1.6, 1)。MD-83的旅客载荷为172,这意味着我们可以使用172Y的全经济舱布局,也可以使用4F10C146Y这种两仓布局。我这里选择添加了当前载荷必须在某个最小载荷和最大载荷之间的限制条件。
# Space constraint
model.addConstr(2.5 * x + 1.6 * y + z <= total_aircraft_space, "space_constraint")
model.addConstr(2.5 * x + 1.6 * y + z >= min(total_aircraft_space * 0.90, total_aircraft_space - 10), "space_constraint")
这里我们添加每周飞行航班量的限制。
# Total flights constraint
model.addConstr(n <= max_flights_per_week, "total_flights_constraint")
这里我们定义收入字段的限制,即某个仓位的收入为仓位数量 * 每周航班数量 * 仓位座位价格。此外,我们添加仓位客流数量的限制。
model.addConstr(x_revenue == x * n * price_first_class)
model.addConstr(y_revenue == y * n * price_business_class)
model.addConstr(z_revenue == z * n * price_economy_class)
model.addConstr(x_revenue <= daily_first_class_passengers * 7 * price_first_class)
model.addConstr(y_revenue <= daily_business_class_passengers * 7 * price_business_class)
model.addConstr(z_revenue <= daily_economy_class_passengers * 7 * price_economy_class)
最后,我我们将目标优化方程定义为总收入的总和。由于总收入是航班座位数量与每周航班数量的乘积,因此这构成了一个混合整数二次规划问题(Mixed-Integer Quadratic Programming, MIQP)。基于这一点,我们需要设置NonConvex为2,否则无法进行求解。
# Objective function using auxiliary variables
revenue = x_revenue + y_revenue + z_revenue
model.setObjective(revenue, sense=gp.GRB.MAXIMIZE) # Maximize positive revenue
# Set NonConvex parameter to 2
model.Params.NonConvex = 2
# Optimize the model
model.optimize()
到这里我们就完成了模型的定义,以下是全部代码。
import gurobipy as gp
def compute_best_seat_configuration(*args, **kwargs):
compute_best_seat_configuration.__globals__.update(**kwargs)
# Create a Gurobi model
model = gp.Model("SeatOptimization")
# Decision variables
x = model.addVar(vtype=gp.GRB.INTEGER, name="x")
y = model.addVar(vtype=gp.GRB.INTEGER, name="y")
z = model.addVar(vtype=gp.GRB.INTEGER, name="z")
n = model.addVar(vtype=gp.GRB.INTEGER, name="n")
# Space constraint
model.addConstr(2.5 * x + 1.6 * y + z <= total_aircraft_space, "space_constraint")
model.addConstr(2.5 * x + 1.6 * y + z >= min(total_aircraft_space * 0.90, total_aircraft_space - 10), "space_constraint")
# Total flights constraint
model.addConstr(n <= max_flights_per_week, "total_flights_constraint")
# auxiliary variables for min between seats and passengers
x_revenue = model.addVar(vtype=gp.GRB.INTEGER, name="x_revenue")
y_revenue = model.addVar(vtype=gp.GRB.INTEGER, name="y_revenue")
z_revenue = model.addVar(vtype=gp.GRB.INTEGER, name="z_revenue")
model.addConstr(x_revenue == x * n * price_first_class)
model.addConstr(y_revenue == y * n * price_business_class)
model.addConstr(z_revenue == z * n * price_economy_class)
model.addConstr(x_revenue <= daily_first_class_passengers * 7 * price_first_class)
model.addConstr(y_revenue <= daily_business_class_passengers * 7 * price_business_class)
model.addConstr(z_revenue <= daily_economy_class_passengers * 7 * price_economy_class)
# Objective function using auxiliary variables
revenue = x_revenue + y_revenue + z_revenue
if ifs_per_pax:
revenue += ifs_per_pax * (x + y + z) * n
model.setObjective(revenue, sense=gp.GRB.MAXIMIZE) # Maximize positive revenue
# Set NonConvex parameter to 2
model.Params.NonConvex = 2
model.printStats()
# Optimize the model
model.optimize()
# Get the optimal solution
if model.status == gp.GRB.OPTIMAL:
best_x = x.x
best_y = y.x
best_z = z.x
best_n = n.x
best_revenue = model.objVal
print("Best seat configuration (x, y, z):", best_x, best_y, best_z)
print("Best number of flights per week:", best_n)
print("Maximized revenue:", best_revenue)
else:
print("No optimal solution found.")
# Dispose of the model
model.dispose()
我们可以试着运行一下这个方法compute_best_seat_configuration来计算新加坡到珀斯的最佳座位排布。
compute_best_seat_configuration("SIN - PER, MD-83",
price_first_class = 2100,
price_business_class = 1100,
price_economy_class = 660,
total_aircraft_space = 172,
max_flights_per_week = 13,
daily_first_class_passengers = 20,
daily_business_class_passengers = 117,
daily_economy_class_passengers = 842)
输出为
Set parameter NonConvex to value 2
Statistics for modelSeatOptimization:
Linear constraint matrix : 0 Constrs, 0 Vars, 0 NZs
Matrix coefficient range : [ 0, 0 ]
Objective coefficient range : [ 0, 0 ]
Variable bound range : [ 0, 0 ]
RHS coefficient range : [ 0, 0 ]
Gurobi Optimizer version 10.0.2 build v10.0.2rc0 (mac64[x86])
CPU model: Intel(R) Core(TM) i7-9750H CPU @ 2.60GHz
Thread count: 6 physical cores, 12 logical processors, using up to 12 threads
Optimize a model with 5 rows, 7 columns and 7 nonzeros
Model fingerprint: 0x76973cf4
Model has 3 quadratic objective terms
Model has 3 quadratic constraints
Variable types: 0 continuous, 7 integer (0 binary)
Coefficient statistics:
Matrix range [1e+00, 2e+00]
QMatrix range [7e+02, 2e+03]
QLMatrix range [1e+00, 1e+00]
Objective range [1e+00, 1e+00]
QObjective range [1e+02, 1e+02]
Bounds range [0e+00, 0e+00]
RHS range [1e+01, 4e+06]
Found heuristic solution: objective -0.0000000
Presolve removed 4 rows and 0 columns
Presolve time: 0.00s
Presolved: 13 rows, 7 columns, 27 nonzeros
Presolved model has 3 bilinear constraint(s)
Variable types: 0 continuous, 7 integer (0 binary)
Root relaxation: objective 1.651664e+06, 6 iterations, 0.00 seconds (0.00 work units)
Nodes | Current Node | Objective Bounds | Work
Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
0 0 1651664.11 0 6 -0.00000 1651664.11 - - 0s
H 0 0 1009604.2400 1651664.11 63.6% - 0s
0 0 1647915.46 0 1 1009604.24 1647915.46 63.2% - 0s
H 0 0 1646069.2300 1647915.46 0.11% - 0s
0 0 1647915.46 0 1 1646069.23 1647915.46 0.11% - 0s
0 1 1647915.46 0 1 1646069.23 1647915.46 0.11% - 0s
* 6 0 6 1647371.5700 1647371.57 -0.00% 1.0 0s
Cutting planes:
Gomory: 1
RLT: 1
Explored 7 nodes (18 simplex iterations) in 0.03 seconds (0.00 work units)
Thread count was 12 (of 12 available processors)
Solution count 4: 1.64737e+06 1.64607e+06 1.0096e+06 -0
Optimal solution found (tolerance 1.00e-04)
Best objective 1.647371570000e+06, best bound 1.647371570000e+06, gap 0.0000%
Best seat configuration (x, y, z): 10.0 60.0 51.0
Best number of flights per week: 13.0
Maximized revenue: 1647371.5699999998
可以看到在每周13班的情况下,使用10F60C51Y的座位排布能获得最高的收益。笔者在多个航线上使用后发现,单架飞机能获得2-10%不等的提升,且可以根据不同的航线演变出2-3种不同的座位排布。还是以之前的新加坡到珀斯的航线为例,在使用了优化过后的10F60C51Y之后,这条航线的收益为$289647,比原来整整提升了17%!

当我们给飞机配备了客舱服务的时候,我们可以从每位旅客身上赚取部分收益,因此可以在计算中加入如下参数。理论上来说,这样会使得我们的模型更倾向于使用旅客人数更多的座位排布,但实际上因为客舱服务收入占总收入太小,所以基本上不会对结果有更多影响。但是在竞争比较激烈的航线上,客舱服务收入至少能给我们带来一定的降价空间,所以还是值得投入的。
if ifs_per_pax:
revenue += ifs_per_pax * (x + y + z) * n

当然,我们所呈现的MIQP问题只是一个基础模型,并未解决所有问题。主要集中在两个方面:价格预测和座位数量的弹性条件。接下来,我们将逐一探讨这些方面。
首先,尽管价格由玩家设定,但模型将其视为输入的常数。然而,在游戏中,旅客对航程的支付意愿是隐藏的变量。在一条航线上,存在一部分愿意高价支付的旅客和另一部分对价格敏感的旅客。另外,航空公司的声誉和竞争对手的影响也会影响座位上座率。这些因素只能通过价格调整来控制。因此,我们最初设定的价格很可能不准确,当我们增加座位后可能会发现上座率下降。笔者一般会使用多次修正价格和调整座位数量去找到最优的座位数量。
在模型中,我们设置了一个硬性约束,即座位数量不能超过每周旅客需求。然而,在游戏中,有时即使某些仓位有空位,增加航班仍会带来收益。此外,大多数情况下,我们不希望为每个航班定制独特的座位布局。虽然在游戏中操作相对简便,但仍需进行多次点击,稍显繁琐。此外,在现实航空运营中,由于座位调整的复杂性和法规限制,航空公司无法随意调整座位数量。因此,后续的优化可能会引入座位数量松弛条件。即使提供的座位数超过每周旅客数,仍可通过增加航班和座位来实现盈利。此外,引入多种标准化的座位布局也是可行的,若优化目标相差不大,则优先考虑标准化布局。
综上所述,本文对AE这款经营游戏及其机制进行了简要介绍。从航线数据和座位优化的视角,笔者探讨了如何实现最佳盈利。通过建立混合整数二次优化(MIQP)模型,我们能够综合考虑客流、机型、价格等要素,制定更为优化的座位配置策略。在现实世界中,座位排布在航空公司的运营中扮演着关键角色。通过优化座位布局,航空公司不仅能提升运营效率和收入,还能提升乘客的旅行体验。
最后,欢迎大家来AE世界里陪我玩耍!我在Realistic World R7等大家!